My Facebook site is finally LIVE!

Hello and Happy New Year to all of my readers!

I'm starting the new year off on the right foot by finally getting my Math Concepts Explained Facebook site up and running!  I'll be updating that site as I add information to this blog, but I also welcome my visitors and followers to comment and ask me questions there whenever they'd like.  I will do my best to provide whatever math help I can!  Please visit and Like my Facebook page and add me to your Friends list!

Perfect Christmas Tree Math

Here's a fun little post for the holidays!  It's not going to teach any new math concepts, though it is a neat demonstration of an out of the ordinary use for mathematics.  It describes mathematically how to decorate the perfectly proportioned Christmas tree.  I can't honestly say that I have tried it myself, though I don't doubt that it might be useful!

A department store in the United Kingdom by the name of Debenhams issued a challenge to the University of Sheffield math students to devise a mathematical algorithm to determine the optimum number of ornaments, tinsel, and lights in relation to the size of the tree, as well as the perfect size of the star for the top of the tree.  Members of the University's SUMS Math group were able to come up with a set of equations that described precisely what the challenge required:

Courtesy of http://www.shef.ac.uk/polopoly_fs/1.227830!/image/formulaslarge.jpg

The students say that the calculation took about two hours to design, though to actually compute the equations is as simple as entering numbers into a calculator.  The stated purpose of the formula is to help holiday shoppers to be smarter when purchasing decorations for their tree, as with this knowledge they will be able to buy the precise number of baubels and lights rather than have a box of extras leftover once the tree is done, or else not have enough and so have to go and fight through the mall crowds to get more.  It also means that people can find the right size angel or star for their tree, rather than guessing and then potentially being way off when they actually get home.  They say that the formulas are versatile enough to apply to large trees suitable for the Royal Family, right down to smaller trees that are more common.  You can check out the original news release here.

It's probably a stretch to think that this set of equations will make it into widespread use, as decorating for the holidays is way more about spending time with friends and family and having good times, rather than looking for mathematical precision in a Christmas tradition.  However, it's a fun exercise to show young math students that demonstrates yet another useful and unexpected use of math in everyday life.

Happy Holidays to all of my followers, and all the best in the New Year!

How to Derive the Equation of a Circle

Continuing from my last post about the Equation of a Circle, here I would like go through an exercise which hopefully explains more about "why" the equation looks the way it does.  The equation of a circle isn't a difficult one to memorize, and the modifications that you can make to it to shift it either horizontally or vertically are very similar to the methods used in translating graphs of functions.  However, the theory behind the equation is very distinctively about a circle.

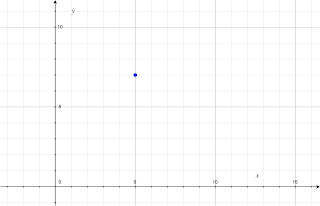To begin, let's start with a point (5, 7).  Now, I ask to find points that are exactly 5 units away from this point.

To begin, it is very straightforward to deduce points that are horizontally and vertically in line with the center point.  We simply move 5 units up and down, and left and right.  This allows us to identify the points (10, 7), (0, 7), (5, 12), and (5, 2).

After these points, it seems that finding new points gets a bit more difficult.  However, it should be fairly obvious that by asking for points that are 5 units away from the center, this is essentially asking for points along a circle with radius of 5.  So then, how to find another set of coordinates (x, y)?

If you pay attention to how I have purposefully drawn the radius in the above picture, you will notice that I have inscribed a right angle triangle with a hypotenuse (radius) of 5.  This is one of the special triangles, a 3-4-5 triangle.  So then, if we then use the dimensions of this triangle, and rotate and flip it around the circle, we can come up with several more exact points that are on the circle: (8, 11), (9, 10), (8, 3), (9, 4), (2, 11), (1, 10), (2, 3), (1, 4).

As you can see, the points that we have identified are beginning to fill out the circle.  But, how can we identify even more (x, y) points?  It doesn't look like there are any points that lie on whole number integer coordinates left.  All that remains are fractional coordinates, and that seems like a lot more work than it's worth to identify more points!  Maybe we can find an expression to more accurately pinpoint ordered pairs, that will include all of those that we've already identified plus all of the ones that we can't?  Let's go back to our picture, and note the generic triangle now inscribed.

If we say that our radius of 5 is the hypotenuse of a right angle triangle, and we already know what the center point of our circle is, then we can do a bit of arithmetic to come up with generic side lengths for our triangle.  If we sweep the radius around the circle, and we always let the inscribed point be called (x, y), then we can state expressions that denote the length of the sides.  In this example, the horizontal side is equal to x-5.  I've visualized this in the following image.

Similarly, the vertical side length of our new triangle can be shown to be y-7.

Now, since we have described a right angle triangle with defined sides, we can apply the famous Theorem of Pythagoras to this triangle (a² + b² = c²).  This means that we can come up with the following equation:

And by now, you should recognize that this is the form of the equation of a circle:

Quite simply, this equation looks the way it does because it is based on the Pythagoras Theorem.  The circle equation really isn't a difficult one to have to memorize, but hopefully this demonstration has shown you the value of triangles and geometry in deriving more advanced math concepts.  Please don't forget to hit the +1 button below, and also follow me on twitter!  You can even click here to tweet about my post.

Credit to a YouTube video by DrJamesTanton where I got the idea for this post.

Equation of a Circle

Once you have worked with functions for a while, inevitably you will begin to wonder "what about circles?"  You have explored all sorts of different equations and their graphs.  Perhaps you've even gone so far as to rotate graphs sideways and learn how to manipulate those equations as well.  But despite these seemingly more involved concepts, you've yet to come across circles.  For such an apparently simple shape, why have these not been included in such rudimentary graphing lessons.

Well, circles are a little different from what you've done so far.  For starters, circles technically aren't functions.  This may surprise you at first, but recall the vertical line test.  Would a circle pass such a test?  Of course not, because passing a straight vertical line through any point on a circle (except for the tangent points on the sides) would also intersect the circle on its opposite side.  Try it and you will see!  So, if a circle is not a function, then how do we handle describing their equations?  That is a little different, but really not much harder than your typical parabola graph.  Follow along and I will explain the equation of a circle in more detail.

For starters, let me just show you the equation for a simple circle.  Consider a circle with a center at the origin (0, 0) with a radius of 1.  We call this a unit circle.  Here is what the equation looks like:

It looks simple, right?  This equation can also be modified using similar concepts to how you would manipulate a function, such as a parabola.  There is a simple change to make to the equation that causes the graph of the function to translate left or right, and a second similar change you can make that results in a vertical translation of the graph.  In this case, depending on where you want to shift your circle, that is the variable you modify.

So, if you want to center your circle at (2, 0), which is a horizontal translation of 2 units to the right, you would change the above formula to include an (x-2)2 term.  Think of it as "if x=2, the whole x term becomes 0.  So 2 is its root."  Same thing applies to vertical translation.  If you change the y term to be (y-5)2, then you can see that the whole y term becomes 0 when y=5, so this means that the circle is centered at a height of y=5.  If we combine these two translations, we shift the circle to have a center of (2, 5), and the final equation looks like this:

Hopefully you can see how easy it can be to locate the center of a circle based on its equation, and how equally simple it can be to determine the equation of a circle just by a visual inspection.  However, to fully describe a circle, there is still something missing.  We haven't looked at what the "1" means.

To fully describe a circle mathematically, the only things that you need to know about it are the coordinates of its center, as well as its radius.  You may think that you should need more information, but think of it as the mathematical equivalent of a geometry set's compass.  To draw a perfect circle with a compass, all you do is put the point down at the center, set the radius, and spin the pencil around the paper.  You only needed those two pieces of information to be able to construct a circle.

Continuing with our example, the radius of our circle is described by the 1 term.  Technically, you can think of it as a 12 term, which provides for our circle to have a radius of 1 (or a unit circle).  To change our radius to 5, we would change the 1 to a 25, because just like the x and y terms, the radius term is also squared.  If we wanted a radius of 7, we would put the term as 49.  In general, this term is r2.

If we put all of these components together, we can come up with the general form for the equation of a circle.  We can include terms that allow for horizontal and vertical translation, as well as whatever radius we want.  Let's call the horizontal shift term "a" and the vertical shift term "b", and the radius "r".  In this case, here is the general form of the equation of a circle:

The equation describes a perfect circle, and doesn't allow for any stretching or compressing along either of the axes.  All that needs to be done is determine the circle's center point and radius, and you can easily fill in the relevant values.

As an example, consider the circle that has radius of 10, and is centered at (-5, 7).  Here is its equation:

Here is the opposite form of the question: what is the center and radius of the circle described by the following equation:

Quick analysis of this by comparison to the general form allows you to find that the center point is (-12, -2) and has a radius of 12.

Hopefully you can see that graphing circles is a little bit different from graphing more familiar functions, though still similar enough that the math concepts we've learned so far can easily be adapted to apply here as well.  In my next post, I would like to explain a little about just "why" the equation of a circle looks the way it does.  For teachers, this is also a good exercise to have students explore when first learning how to graph circles.  

Remember to please click the +1 button below to share my post!

How to use LaTeX Equation Editor

This is a post aimed at anyone who has a reason to type math symbols.  It is about the LaTeX equation editor, which is an online math utility.  I'm sure that many people know of this already, but it was only recently shared with me, and so I would like to share with anyone else who will find this valuable.  In particular, those who I feel this will benefit are: teachers and education professionals; students doing math homework; graduate students preparing thesis material.  Of course, anyone having to put any kind of math equations into a document will appreciate this.

The LaTex math symbol code generator can be found online at http://www.codecogs.com/latex/eqneditor.php.  It's a little intimidating at first glance, but after a little bit of experimentation, you should be able to generate any math equations that you can write down on paper.

In the upper control panel, you can select the functions that you wish to include.  For example, if you click the a/b button (left side of the panel), this is the generator for a fraction expression.  You can put any level of detail into the equations, and nest them within each other as necessary.  When you select the function, you will see a code for that function appear in the large main rectangle directly underneath the control panel.  When you become a LaTeX professional, you can just type your function codes directly into this box.  Once you click the function buttons to generate code, you will also find sets of brackets {}, in which you can type numbers, letters, or insert additional function codes.  Beneath the box, you can find some formatting options, below which you will see your math expression, rendered as an image .gif file.  You can copy this image, and then paste it into your document.

For example, if I want to generate an image for y=mx+b, rendered in a nice, textbook-like font, here is how you would do it.  This is a very simple example.  All you would do is type this in the box, and then observe the rendered image below.  This one doesn't require specific selection of functions from the control panel.  Here is what it looks like:

Note how much more professional it looks, compared to regular in-line text.

Another example will demonstrate the function abilities.  Let's try to write y=x² + 2x + 1.  First, I would type "y=x" and then click the x^a function button, which denotes exponents.  This would make your code look like "y=x^{}".  Into the brackets, you click and type a 2, and then you can move the cursor to the end and just finish typing the remainder of the equation.  The final expression looks like this: y=x^{2}+2x+1, and here is the image file:

To make a slightly more complicated functions, let's try to write y = x^2/3/4.  You have to build complex equations from the outside-in.  So type "y=" to start, and then we need to select the fraction button, the a / b button.  That displays the code "y=\frac{}{}".  In this case, you type the numerator in the first brackets, the denominator in the second brackets.  However, the numerator has a fraction in it.  So, you click within the first brackets, and then type x and then add the new function, the exponent one again.  Into the additional brackets that appear, you can type 2/3, and then in the final set of brackets, type the 4 for the denominator.  Here is what the code looks like for this one:  y=\frac{x^{2/3}}{4}, and here is the image:

The best part about this code generator is that it updates the .gif file in real-time, so you don't have to type out a huge, complicated expression, and then hope you get it right.  If you make a mistake, you will see it right away, and then you can modify as necessary until you get what you want.  When you have it correct, you can right-click and save the equation image as an individual file, and then immediately erase your code and start over again with a new equation.

I find the LaTex equation editor to be extremely helpful, especially here on my blog when I want to show more complex expressions.  It does require having to go to a separate website, typing your code, and then coming back to your original document and inserting a file.  So, for ease, I often will just type straight text into my documents.  However, for that extra professional appearance, you cannot argue that the generated codes look fantastic!  If you have never used this before, I highly recommend that you give it a try!  If this is new to you, as it was to me recently, and you find value in this, then please click the +1 button below to share this!

Minimum Distance Between Two Parallel Lines

A lot of students seem to have difficulties in determining the minimum distance between two parallel lines.  Conceptually, if you have these two lines next to each other with the same slope, you can draw any number of different lines that can connect the two, though they all would be at different angles.  However, the shortest line that you can draw is the one that is perpendicular to them - the line that has no relative side to side travel to add extra length to the connecting line.  This post will hopefully explain simply how this can be done, while showing that it isn't really anything more difficult than identifying the information that you need, and then using a series of simpler concepts to get to the final solution.  You will hopefully find that these problems really aren't that difficult!  Please do me a favor and click the +1 button at the end to help me share my post!

Sometimes you will be given two lines (or line segments) or an equation to start with.  Here, let's start even further back, just for practice.  Let's begin just with two random ordered pairs that I've selected.

Find the equation of the line AB that crosses through the points A(2,1) and B(4,6).

As I described in my previous post here, you can determine the equation of this line quite easily.

Slope m = (y₂-y₁) / (x₂-x₁) = (6-1) / (4-2) = 5/2

Y-intercept b = y-mx = 1-(5/2)*2 = (-4)

Therefore: y = (5/2)x - 4.  This is the equation of our line.  You shouldn't have had problems following along through this step, though if you'd like some review, check out my post here.  Now that we have our first line, let's develop the rest of our problem.

What is the minimum distance between line AB and a parallel line CD that passes through point C(3,8)?

Recall that parallel lines, by definition, are lines that have the same slope, and so will never cross or come closer together.   Also, though you can fit any length of line in between these two starting lines, the shortest one you can draw between them is perpendicular.  Draw two lines and convince yourself of this!  The minimum distance between the two lines is a line perpendicular to them both. 

Here is a small recap of the information that we already know to help us answer this question, as well as a bit of an outline of how we will go about solving it.

Finding the distance between our line and point

• First line: y = (5/2)x - 4
• Point on second line = (3, 8).  FYI, you now have enough information to determine the equation of the second line, though it's not required right now.
• Shortest distance between the lines is an intersecting line that is perpendicular to both. 
• The distance can be calculated by the distance formula. What does this need?  We need two points. We have one given to us, and now we need the second point, which will lie on our first line.
• We find this second point at the intersection of the starting line and the perpendicular line that passes through the given point. How do we find this intersection?
• The intersection is where the equations of the two lines are equal.  We have the first equation, solved in the first step above.  How do we get the second equation, of the perpendicular line?
• The second equation comes from knowing the given point, and the slope perpendicular to our parallel lines.  Recall: the slope that is perpendicular to slope "m" is "-1/m".
• Solving the system of equations will yield our second point of interest.  And once we have the point, we can simply plug numbers into the distance formula to find our final answer.

It seems like a lot, but if you follow it through, you can see the logic behind all of the steps. Find one thing which leads to another, which leads to another, which leads us to the solution.  This is another good piece of advice for working with more complex problems.  Look at what you need to find, and try to step backwards to identify helpful steps that you can take to progress through the process. Ask yourself "what do I need to find this?" and then "what do I need to find that?" and you will then find that you have outlined your own strategy of how to solve the problem!

So then, let's get to the numbers.  To start, let's find the equation of the perpendicular line.  We have a point (3,8), and we want the slope that is perpendicular to the slope (5/2)... which is (-2/5). Now we can find our equation.

(y-y₁) = m(x-x₁)

y-8 = (-2/5)(x-3)

y=(-2/5)x + (6/5) +8

y=(-2/5)x + (46/5)

Our line and point, with the perpendicular minimum distance shown.

Now we want to find the intersection point of this perpendicular line with our first line (equation y=(5/2)-4). To do this, we solve the system of equations by setting them to be equal to each other, solve for the variable x, and then sub in this x value into either one of the original line equations to find y.  x and y are the ordered pair of our second coordinate.

Solve the following system:

y=(5/2)x - 4
y=(-2/5)x + (46/5)

(-2/5)x + (46/5) = (5/2)x - 4

(-2/5)x - (5/2)x = (-4) - (46/5)

(-4-25)x/10 = (-20-46)/5

(-29)x/10 = (-66/5)

x = (-66/5)(10) / (-29)

x = 660 / (5)(29)

x = 132/29 Here is our x value! (Kinda ugly, but sometimes that's what you get!)

Now we put that value into either one of the first two equations in our system, and solve for y.  Both will give the same answer... they have to! We're talking about the POINT where the two lines cross, and hence are EQUAL in both cases.

y = (5/2)x - 4

y = (5/2)(132/29) - 4

y = 660/58 - 4

y = (660 - 232) / 58

y = 428/58

y = 214/29 Here is our y value! (Just as ugly as x!)

Here's our system, with the intersection point now displayed.  Looks like our calculations are correct!

So, we have our point on the first line as (132/29, 214/29).  Now all we need to do is find the distance between this point, and the given point (3,8).  To do this we can use the distance formula.  I've explained the distance formula in another post, so I'll just go ahead and use it here.

distance, d = sqrt[(x2-x1)² + (y2-y1)²] 

(Again, my apologies for not being able to show a proper square root sign.)

d = sqrt[(3-132/29)² + (8-214/29)²]

d = sqrt[(-45/29)² + (18/29)²]

d = sqrt[(2025+324)/841]

d = sqrt[2349/841]

d = (9/29)*sqrt(29) This is the answer!

Unfortunately, we get a nasty looking answer.  But that doesn't make it any less correct.  Hopefully you were able to follow along with how I approached this problem, and how we arrived at the solution, because these are the kinds of steps and logical thinking that you will need to use.  In all likelihood, most questions that you will encounter in your math studies are going to look a whole lot friendlier than this monster.  As always, feel free to leave any comments or questions below, and I'll do my best to address them. :)  Also, please remember to click the +1 button below if this was helpful.  You can even tweet about it automatically by clicking this link.  Bookmark my site and come back again!

What is Perpendicularity?

"Perpendicular" is the term used in mathematics to describe two lines that intersect at right angles.  I recently introduced this concept in a separate post about the definition of perpendicular lines, but I thought it might be interesting to go into a little bit more detail about this rudimentary and familiar math concept.  For students who are just learning about graphing lines for the first time, this is undoubtedly sufficient, but for those more familiar with the concept, this post might provide additional insight.

I opened above by stating that we are talking about two intersecting lines that form a 90 degree angle with each other, though this definition can and should be expanded.   Though technically correct, there is more to the concept of "perpendicularity," as it's called when talking about this subject.  More correctly, this term applies to not only lines (and line segments), but planes (surfaces, not airplanes!) as well.  At first this may sound advanced, but if you think about it, it is completely obvious. If you stack two books together in a perpendicular arrangement, you essentially are viewing the intersection of two planes.  Lines are drawn on paper, but planes are like the three-dimensional versions that have depth., and you can readily find examples in real life of things that are at 90 degrees to each other.

That leads me to a second point about perpendicular lines and planes.  I have said that they intersect at 90 degrees, which is true again, but more accurately and mathematically you can say that the lines form two "congruent adjacent angles" (Wikipedia link).  This means that if you look at the perpendicular intersection in a T-shape, you see two angles next to each other (adjacent) that are the same (congruent).  And by the rules of geometry, since the angles along a straight line must add up to 180 degrees, this obviously means that the intersection must be composed of 90 degree angles.  Furthermore, if the lines extend through each other, the rules of geometry state that all angles around a point must sum up to 360 degrees, so again we have 90 degrees for each - four right angles.

Perpendicular lines

Perpendicular planes

Here's some additional information that you might find interesting.  The term "perpendicular" itself can be an adjective describing the lines, as in "the perpendicular lines are written in red ink."   Alternatively, it can be the noun, as in "the perpendicular to the ground rises to the sky."   Sorry, those examples aren't very creative!  Also, another word for perpendicular is "orthogonal," which can be used the same way to describe right angle intersections.  "Orthogonality"comes from the Greek for "straight angle" and refers to lines and planes at ninety degree angles, much like "perpendicularity."

I know these math definitions probably aren't going to make solving your graphing problems any easier, but I thought that it was good information to know!  It's a very important but basic concept that is introduced very early in math education, so hopefully I have explained it simply enough even for beginners to grasp.  Please click the +1 button below to share my post, and you can even tweet about my site if you like it!

Definition of Perpendicular Lines

A lot of traffic coming to my site lately has been specifically seeking to learn more about perpendicular lines.  At this point in the new school year, many math classes are just beginning to study graphing, and so perpendicular and parallel lines are often discussed along with other basic graphing concepts, such as slopes and intercepts.  In this post, I would like to give you a definition of perpendicular lines, maybe include a bit of review of some other graphing notes, and go over a few example questions involving them that you are almost guaranteed to encounter in your mathematics courses.  By the end of it, you should be an expert at recognizing and graphing perpendicular lines.

Let's start with the perpendicular lines definition.  It specifically is talking about the relationship between two different lines who intersect at a 90 degree angle.  Two lines that cross at 90 degrees are said to be perpendicular to each other.  A good example of this is the familiar x-y axis.  The y-axis is perfectly up and down with absolutely no slant to the side, whereas the x-axis is perfectly left to right with absolutely no deviation to the vertical.  You can easily see that they form right angles where they meet.  However, it is important to realize that the lines themselves can go in any direction, not strictly up/down and left/right.  The only critical part is that they intersect at 90 degrees.

On a side note, a corollary to this definition is that the four angles created by the intersection of two perpendicular lines are all 90 degrees.  Comparatively, the intersection of two non-perpendicular lines results in the formation of two acute angles (less than 90 degrees) and two obtuse angles (more than 90).  This also demonstrates the geometric law which states that the sum of the angles around a point equals 360 degrees.  This is a useful rule to remember when solving geometric proofs.

So then, now that you understand what this word means and how to visually recognize it on a graph, you may then wish to prove that your two lines do indeed meet the criteria.  How would you even go about that?  How can you determine if two lines are perpendicular?  Well, to do this, you need to know the mathematical equations of the lines… or, more specifically, you need to know the slopes of the two lines.  (Recall that the slope of a line is most simply expressed as "rise over run", which represents the ratio of vertical change to horizontal change.  The slope of the line, often abbreviated by "m", is easily solved by comparing two ordered pairs, and then performing the slope calculation m = y₂-y₁ / x₂-x₁.)  True perpendicular slopes will have the following relationship:

m₁ = -1/m₂

In words, this means that the slope of the first line is equal to the negative inverse slope of the second line.  Looks a bit complicated, but it's not really.  Let's take a look at an example.

Consider the lines described by the equations y = 2x - 1, and y = (-1/2)x + 2.  Are these perpendicular?

This is an example of perpendicular lines.

If you want to get some practice graphing perpendicular lines, you can go ahead and plot these curves.  They are already expressed in standard form, so it is simple to determine the slopes and y-intercepts, and you can also readily generate a table of values to plot points along the lines.  That's a great way to show that you know how to graph the lines, and in the end, you would end up with two lines crossing at 90 degrees.  But that would take an awful lot of time on a test to find a solution that can be found much more quickly and easily.  Just consider the relationship that I explained, and see if it is true in this example.  You can see that the slope of the first line is m = 2, and the slope of the second line is m = -1/2.  This precisely fits the mathematical description of perpendicular lines.  You don't even technically need to graph it out to be able to answer this!  Of course, a wise plan of attack for solving this problem would be to check this relationship first, and THEN graph it out to show that you are correct.  This comes from personal experience.  Always check your work!  ;)

With this information, you should be able to see that all you need to know about lines are their slopes to be able to say whether they are perpendicular or parallel.  Recall, parallel lines have the exact same slope.  The trick when working with this type of question is to realize the the intercept values can be 2 and 3847234, or absolutely anything else at all.  They equation of the line may look completely and extraordinarily different for each, though the only important part of them is their m values.  Keep this in mind, and don't get intimidated by complex and scary-looking equations!

Another type of question might ask you to determine the equation of a line perpendicular to a given line through a specific point.  This takes a bit more work, but it is based on the same concepts.  Let's try a question like this.

Find the perpendicular line to the line y = 2x - 1 that goes through point (4,0).

Here's the approach I would take to solve this.

1. First, recognize that you are given one of the lines' equations, so from that you can easily find its slope. 
2. Second, from the first slope, you can use the perpendicular relationship to determine the slope of the second line.  
3. Third, since you now have the slope and a point that lies on the second line, you can substitute numbers into y = mx + b to solve for b, and then rewrite in in terms of x and y to give the final equation.  

I will leave the actual work for you to try yourself, but the line in this case is the same as above, y = -1/2x + 2.

A third type of question might ask you to determine the perpendicular bisector for a given line segment.  A bisector is a line that perfectly splits another line into two equal pieces, but it can slice through at any angle.  On the other hand, a perpendicular bisector is one the does this at precisely 90 degrees.  If you can first determine what the exact midpoint of your line segment is, you can then apply the approach that I outline above to solve this question as well.

There is one last important point that I would like to make about this topic, and it is about notation.  You are not incorrect to simply state that "line AB is perpendicular to line CD" (or whatever your lines are called), but the shorthand symbol to show this is an upside-down T shape, ⊥.  The keyboard character is called the "up tack", though this term is more applicable to lattice theory, type theory, and logic.  I believe it is more appropriate to simply call it the "perpendicular sign."  So, in this case, you would simply state your answer as AB⊥CD.  That's it.  It's much simpler!

Finally, I thought I would just throw in a bit of trivia that I came across while researching this topic.  Who knows… you might be able to impress your teacher!  The word "perpendicular" originally arose in the late 14th century, and its etymology shows that it came from the Latin word "perpendiculum", which means "plumb line", and "perpendicularis", which means "vertical, as a plumb line".  A plumb line was a simple device which was composed of a small weight on the end of a string, and when holding it up, gravity pulls the weight straight down and the string represents perfectly vertical.  In relation to the ideally perfectly horizontal ground, you can see how they came up with this term.  It's not overly useful information, but you never know where extra trivia might come in handy.

So, with that information, you should now know lots about this subject, and now have no problems graphing perpendicular lines or analyzing and identifying them in either graphs or equations.  There are several different variations to the questions that you may encounter, but if you understand the basics of what it is that defines two perpendicular lines, then you should have no problems in coming up with the appropriate solutions!  Please let me know in the comments below if you would like any further explanation or examples, and don't forget to +1 my post below and follow me on Twitter!  I'm @MathConcepts.  You can even click here to tweet about my post!  Be sure to visit my follow-up post that discusses a bit more of this concept of perpendicularity.

Standard Deviation and Variance - Statistics

I've already discussed several of the ways that you can represent the center of a distribution.  I've also already presented to you the concepts of variability and spread of the data; I explained in my last post percentiles (and by extension, quartiles), and then how these points can be used together with the center and extreme values to provide you with a five-point overview of your distribution (shown in the box and whiskers graphs).  However, a far more common way of describing the spread of your data is by reporting the standard deviation.

The standard deviation provides a different view of the spread of the distribution.  Instead of reporting certain points within the data set (as with the box and whiskers plot), the standard deviation is essentially an average measure of how far away each data point is from the mean of the data set.  Quite literally, it indicates how far the data "deviates" from the mean, or, how close all the data is to the mean. Think about what this is saying, and hopefully you can see how this also appears to be a good way to describe how wide the data is spread.  For any normal, or bell-shaped distribution, a smaller standard deviation means that you will have a narrower peak, since most of the data is close to the mean.  Alternatively, a large SD would mean that the distribution is fatter and more spread out.

Unfortunately, these calculations require rather tedious formulas, if doing the math by hand.  Thankfully, calculators often have shortcuts, but I will leave that with you to explore on your own calculator.

To begin, I first need to make a comment about the notation that I am going to use. Much like what I said in the discussion of sample mean vs population mean, the standard deviation and variance statistical functions can be used when talking about either smaller samples of populations, or entire populations. Being so, they also have differing notations to designate which distribution is being analyzed:

• When talking about a population, standard deviation is denoted by "σ" (sigma). 
• When talking about a sample, standard deviation is denoted by "s". 

To calculate the standard deviation (manually), you must first find the mean, and then you find the variance of the data set, and from there you only have one final, simple operation.  Here is a general definition to mathematically describe the variance and standard deviation: The variance is equal to the average squared deviation from the mean, and the standard deviation is simply the square root of the variance. Sounds simple enough, right? Here is the formula you use to calculate the sample variance, which (logically enough) has the symbol of s²:

Notice how this is similar to how you would calculate an average.  You sum up "n" values, and then divide by the number of values.  In this case, however, there is a very important point to make.  When calculating these statistics for a SAMPLE, you use the term "n-1" instead of "n".  This is essentially a correction factor that is used, to account for the fact that not the entire population was used in the analysis.  When finding a POPULATION variance and standard deviation, it is a truer average because in that case, you do divide by the total number of units.

Since the numerator of this expression is just a large sum, we can also rewrite the formula using the shorthand "sigma" notation that I demonstrated previously in my post about means:

As I said above, if you have done all this hard work to find the variance, the standard deviation is a simple step away at this point.  All you need to do is take the square root of both sides.

or

I know... these expressions and concepts look messy and complicated.  And if you have a large data set, it can get very cumbersome to perform these mathematics by hand.  In those cases, calculators are extremely helpful, or better yet, a spreadsheet program like Excel.  However, as I've said several times, it it very beneficial for you to understand how to do things like this the long way before you learn to take the shortcuts later.  It ensures that you have a solid grasp on the math concepts at work.

In this case, it may help to not think of the formulas as they are written, but rather as what they are trying to do.  In general, you are just adding up the squared distances of each data point from the mean, and then dividing by a whole number of data points, paying attention to whether it is a sample or population.  By simply doing that, you are finding the variance first, which you can then easily use to determine the standard deviation.

But you now are probably asking "just what does the standard deviation tell me?"  Beyond the general definition I gave above, here is a bit more information that you will find useful in understanding these concepts better.  If you have calculated the standard deviation as outlined above, you have solved for s (or, for 1 times s).  One standard deviation away from the mean represents about 68% of the data set, two SD's (or 2 times s) encompass about 95%, and three SD's include almost 99%.  From this, you can now also relate the standard deviations to the general shape of your distribution (i.e. is it wide or narrow?).  I found that Robert Niles' website has quite a helpful discussion on this topic.

So, now hopefully you have a better understanding of these common statistics!  You will use these stats countless times in your mathematics studies, so I really hope that I have done a decent job explaining what is going on, if not at least just how to go about doing these analyses!  Remember, I really appreciate the social shares if you found any values in my posts!  Thanks!

Percentiles, Quartiles, and Measuring Spread - Statistics

I recently explained several math concepts relating to the measurement of the center of data.  I explained the differences and how to obtain the mean, median, and mode for a set of data. While these statistical functions are indispensable when assessing how a data set is centered, they tell you nothing about how that data is spread out, or the variability.  To get this information, percentiles and quartiles are frequently used to supplement what you have determined about the center.

To better understand why knowledge about your data's center isn't sufficient, and why we need to know about the spread of the data as well, consider this point.  If you have a data set A composed of values 36, 38, 40, 42, 44, you can easily determine that the mean (center) of this set is 40.  Now consider a data set B that has the values 0, 20, 40, 60, 80.  This set also has mean of 40.  However, even though these two data sets have the same center, they are obviously very different!  Set A has a much tighter and narrower distribution, whereas set B has a much broader range.  This is where an analysis of the spread of the data is important to better understand your distribution of data.  Having information about both center and variability of your data distribution is one of the simplest and most useful analysis there is.

To start this discussion, I will begin with where we have already been: the median.  I explained that the median is the midpoint of your ordered data set.  So, 50% of your data points are below your median, and 50% is above it.  Now, from here, let me introduce the concept of quartiles first.  Personally, when I think of quartiles, I think of quarters immediately.  If a median is at the point representing 50% of the way through your data, the quartiles represent the points that are quarters through your set, or (roughly) every 25%.  So, the first quartile (called Q1) is at the point 25% of the way along your ordered set of data points (or, it is larger than 25% of the data, but still smaller than 75%).  It is better to say this is the median of the data on the left side of your overall median.  On the other end of your data is the third quartile (Q3), representing the 75% mark of your data, where it is larger than 75% of your group but 25% is greater still.  Similarly, you would find this by finding the median of the data that is to the right of the overall median.  And for those astute enough to catch that I skipped over the second quartile, it is true that the second quartile is the same as the median (M), at the 50% mark.  So, from this, you can hopefully already see that you can get a good idea of the spread of your data with this brief analysis.  (Technically, I refer to these points as 25% and 75% marks, though I recognize that these are approximations.  It is more appropriate to think of them as medians of each half of the data, and if you do the math to say they are the x-th value out of n-values, you will find that they are around 25 or 75, but likely not exactly.  I say this here not to confuse you, but because I'm sure some of my readers will point it out to me!)

In many cases, to get a good overall view of your data, you can report the mean of your data alongside the first and third quartiles.  In addition to this, it is also good practice to report the lowest and highest (extreme) data points.

With this information, you can construct a box plot (also known as a box and whiskers plot) that conveys all of this information visually, at a glance.  Box plots are extremely helpful, especially when you can present data sets side by side for easy visual comparison.  A box plot has a mark to denote the median, inside a box that represents the range from the first to third quartile.  You can alternately think of it as being a box of the quartiles, with one edge on the first quartile, the other edge on the third quartile, and a line inside the box to denote the second quartile.  Extending past the edges are lines that end on the extreme values.  Think of the box are representing the bulk of your data (more technically, the middle 50% of your data), which is why it's thicker, and the lines on the ends represent only a thinner amount of your data, or the tails of your distribution.

Follow along below to see an example of what a box and whisker plot looks like.  This hopefully demonstrates all that I've talked about above.  Note that the center, quartiles, and extremes are all easily seen on the box plot graph, and how easy they are to compare when presented like this.  

Consider the following two data sets, and then follow along with the analysis:
Set A: 32, 5, 8, 12, 2, 6, 2, 35, 32, 15, 18, 25, 22
Set B: 33, 1, 8, 33, 32, 26, 1, 18, 1, 30, 28, 29

The first thing you have to do for this statistical analysis is arrange the data from lowest to highest.

Set A: 2, 2, 5, 6, 8, 12, 15, 18, 22, 25, 32, 35
Set B: 1, 1, 1, 8, 18, 26, 28, 29, 30, 32, 33, 33

Now, you can just count off the important points.  Here, we have a relatively small number of points in each set, so it is easy to find these important marks.  I will colour them below:

Set A: 2, 2, 5, 6, 8, 12, 15, 18, 22, 25, 32
Set B: 1, 1, 1, 8, 18, 26, 28, 29, 32, 33, 33

It is a good method to draw yourself a number line, and then use it to construct your box and whiskers right above it once you've identified your important points. Here is how you could progress through the creation of this plot, along with the final result.

As you can see, you can gain a lot of information about your distributions very quickly!  You can see that Set A has a lower center, and a narrower spread (less variability).  Compare this to Set B, which has a higher center and a much broader range.  Note that the extremes are very similar in each case, so despite having similar ranges, these distributions are quite different.  One is smaller and tighter, the other is higher but broader.  Hopefully that explains quartiles for you!

Now I will briefly extend this concept to percentiles.  Technically, quartiles are only a subset of the percentiles. They represent the 25%, 50%, and 75% (roughly) marks of your set.  Percentiles, on the other hand, can represent any position in your data.  You can talk about the 95th percentile, which indicates the point that is greater than 95% of the rest of your data, or the 7th percentile where it is greater than only 7% of your data (and through induction, smaller than 93% of your data!).  You just have to determine which of your data points represents the percentage you want, and you have it!  If you compare this to how I explained the quartiles above, you can see that it is the exact same concept applied to any point that you want!  The quartiles have a special name simply because they have historically been used the most often.

So, with that information, you hopefully can now understand the importance of measuring the variability of your data in addition to measuring its center.  You can gain a lot of useful information from this simple data analysis, and it provides a great place to start when you are performing any amount of statistical analysis on a distribution of data.

In my next post, I would like to extend my discussion of data variability of data to include one of the most well known statistical functions: the standard deviation!

Sample Mean vs. Population Mean

I did not mention this is my last post that outlined some basic statistical functions related to central tendency, but when studying stats, it is important to understand that you will be dealing with two kinds of means: a sample mean, and a population mean.  Conceptually, they both do the same kind of thing, though their meanings are slightly different.  It is a very good idea to know when to use sample mean vs population mean, and I will try to go over these concepts and their uses in this post.

Mathematically, I already explained how you determine a mean value.  It is what you have likely always known as an average value, and you can very easily find it using the mean formula.  Without actually writing out the equation, you already know that the mean is the sum of all your values, divided by the total number of your values.  This is straightforward and nothing new.  Here is where I am going to make a distinction that you need to be aware of.

In statistics, you deal with populations.  Populations are complete groups of people, of things, of measurements.  As an example, you likely know of the population of the planet Earth.  That refers to all of the people on the planet.  Or, you could have a population of bald eagles in a nesting ground, or a population of Ferrari sports car manufactured in 2011.  Populations refer to the whole group of whatever you are talking about.  However, in many cases, you don't have access to data about the entire population.  You only have access to a subset of that population... a sample of the population.  So, a sample can be considered to be a small part of the population, but is representative of that population as a whole.

A sample could also be looked at as only an estimate of the larger population.  They are frequently sufficient enough to work with, since having data for an entire population could involve a very complicated and long set of data, and the closer your sample size is to your population size, the more accurate this estimate becomes.  This is why people tend to question things that are only based upon a few observations... error is higher when sample size is smaller.  More observations means less error.

So then, with those definitions in mind, you should hopefully be able to understand what is meant by population mean and sample mean.  Literally, a population mean is the average of the entire population, whereas the sample mean is the average of a sample (which represents a larger population).  Of course, since this is mathematics, we have different ways to write the notation for these two statistics concepts.

When we are talking about a population mean, where we have data about all of the subjects or measurements of a given population, we represent that data by the Greek letter mu, which looks like a fancy lower-case u:

This is calculated by summing all of the values in the entire population, and then dividing by the total number of values in that population, which is denoted by a capital N for a population.

On the other hand, when we are dealing with a sample mean (a subset that is representative of a whole population), we denote this function by the aforementioned symbol, x-bar:

As before, we find this by summing all of the values in your set, and then dividing by the total number of values in your set, in this case, the number being denoted by a lower-case n for a sample.

As I mentioned, calculating these values means essentially doing the same thing.  However, in stats, it is wise to pay attention to the group that you are analyzing.  Making a mistake at this point could lead to much larger errors in any further statistical analysis.  Keep in mind that a sample mean is an approximation of a population mean, and that approximation becomes more accurate as the size of your sample (n values) approaches the size of your whole population (N values).

Central Tendency - Statistics

In this first post of my new Statistics series of posts, it is going to be a refresh of the most common statistics you have ever done (and perhaps didn't realize were actually statistics): measures of central tendency.  I've previously done posts that briefly described the functions that measure center (e.g mean, median, mode), but here I am going to compile them all together in one place, and provide perhaps a better explanation of these statistics concepts.

Mean

The first statistic that I include here is the most common statistic with which you have likely ever worked.  You probably know it be the name "average" but in the field of statistics, you will find it referred to by "mean," "arithmetic mean," or "arithmetic average."  It probably doesn't need much of an explanation, as most students learn how to calculate averages very early on in school!  It represents a calculated measure of the center of a distribution of values, simply obtained by adding up all of the values and then dividing that sum by the number of values you added together.  (It is important to be aware that there are different types of means in statistics: sample and population means. I describe these in more detail in a separate post.  For the sake of demonstration, consider the math in this post to describe samples instead of populations.)

There are a couple of important points to make about the notation involved in calculating means.  The first is regarding the actual mathematical symbol for mean (because you don't want to always have to write down the word "mean" in your solutions!).  The symbol for mean is written as an x (or whatever variable you are using) with a small horizontal bar over it, like this:

You say this symbol as "x bar."  You can use and will see this notation wherever an arithmetic mean value is being used in statistical analysis and calculations.  It is extraordinarily common, yet would appear confusing at first to a student who is new to statistics, because it looks like nothing they had ever dealt with before.

In addition to this, there is a second notation that you will see that may need an explanation first.  This notation is used to describe the arithmetic mean formula.  I explained the concept and process of calculating a mean above, but here is one way in which you could write this down in your work:

Mathematically, this simply says that the mean is equal to the sum of all your values (x₁ all the way up to x_whatever) divided by the total number of values that you are adding up.  This average formula could also be represented in another way, like this:

This formula for mean is saying the same thing as the previous one.  The 1/n part is the same in both equations (in the first, dividing by n is the same as multiplying by 1/n).  The fancy capital E-looking thing is the Greek capital letter sigma (which is not equivalent to E, but rather to S), and in math, it means to "sum up everything in the following equation."  And the x_i part represents all the values of x.  So the sigma would start with x₁, then add x₂, then add x₃, and so on, for all the values of x.  (I will do a separate post on sigma notation to perhaps explain this a bit better, with more examples.)

An important concept to understand about the mean is just what exactly it represents, and how it can be influenced by its dataset.  For a collection of values that are similar, the mean will provide a fairly reasonable measure of the center of this data.  However, if you consider the inclusion of any extreme values, you can see how this would cause the arithmetic average to be biased in its direction.  The more extreme the outliers are, the greater their effect on the mean.  Try for yourself to see what I mean.  Consider the dataset of values 1, 2, 3, 4, 5, and then consider the dataset of 1, 2, 3, 4, 20.  You can see that the mean is pulled in the direction of the outlier.  This is simply a result of how the mean is calculated, and is one of the flaws of it as a statistical tool.  Similarly, if have a distribution of values in your dataset that are "skewed" (that is, if you graph them out, you will see that the graph isn't symmetrical, and it has a tail on one end), the long tail will tend to bias the measurement of the mean in its direction.  Because of these characteristics, the mean is considered not to be a resistant measure (in that it can't resist being pulled by extreme data).  However, despite these points, the mean is an incredibly useful tool for statistics, if for no other reason that it is so simple to use, and provides a very quick evaluation of how the dataset is centered.

Median

The median is a second of the three measures of center that I want to talk about here.  Conceptually, I think that it is probably even simpler to understand than the mean.  It's much easier to calculate.  Whereas the arithmetic mean requires you to perform the calculation I described above (or really keen people know how to use their calculator's mean calculation function!), to determine the median, you don't have to do any mathematic operations at all!  Quite basically, the median represents the midpoint of your dataset, the point where half of the data is larger and the other half is smaller.  You don't have to calculate it, you just have to identify it.

To do this, all you need to do is take your dataset, and arrange all of the values in increasing size.  The value in the center is your median, often represented by the capital letter M.  When you have an odd number of values in your dataset, you will be able to find the median very easily.  You can identify it through a quick calculation to find which is the center value, which is simply the (n+1)/2 value in your order, where n is the total number of values in your dataset.  Note that this median formula only tells you where in the order your median is located, not the value of the median.  If you have an even number of values, then your median is represented by the mean of the two center values (using the same calculation above to determine the location, you'll result in a location 4.5 for example, indicating that the median is the mean of the values at locations 4 and 5).  So, in this case, your median does not necessarily have to be one of your data points, but instead the average of the middle two.

Determining the median can be a very tedious process if you have a very large dataset.  In these cases, the use of a spreadsheet software will come in extremely handy!  Then, you can automatically sort your values, and then identify the one(s) you require.  For small data sets, on the other hand, it takes very little effort to sort through and rearrange the values, making the median another very simple and useful statistical tool to evaluate central tendency.

There are a few differences to consider when comparing the mean and the median.  Since the mean uses the actual data values in its calculation, it is influenced more by extreme or skewed data.  Therefore, the median will represent a better estimate of the center of the distribution.  In this sense, the median can be considered to be a more resistant measure than the mean.  So, if you have a symmetric distribution of data, the mean and the median will be very similar.  However, when you have skewed distributions, the mean will be located more in the long tail of the distribution, further away from the median.  Consider, if you have a set of prices in a data set, and then you double the highest price, the median will be the same in both cases, though the doubled price point will push the mean much further away and more towards that extreme end of the distribution.  The mean and the median provide differing assessments of the central tendency of a distribution, but both functions are extremely useful in statistical analysis.

Mode

The mode is the third statistical function used to evaluate the center of a dataset.  It is just as easy to determine as the median.  Once again, there is no mathematic operation needed to determine the mode.  That is because the mode is quite simply the value that is most common in your dataset.  If you have arranged all of your data points in increasing order to assess the median, as described above, then it is quite easy to find the mode.  For example, in the dataset 1, 2, 3, 4, 4, 4, 5, the mode is 4 because it is repeated the most often.  See?  Easy!  

There are two points to keep in mind: for one, you can have more than one mode (if you have a dataset of 1, 2, 2, 3, 4, 4, then you have two modes, 2 and 4); and second, if no term is repeated at all, then there is no mode to the dataset.  

It is also good to know that of these three statistical functions I've covered already, the mode is the only stat that can be applied to non-numerical datasets.  For example, the mode could be used to say what colour shirt is the most commonly worn shirt in an office.  The dataset for this could read like: red, white, blue, green, blue, yellow, blue, blue, red, black, and so the mode is blue.  You can't arrange these in increasing size to find a median.  You cannot apply the mean formula.  These concepts don't make any sense when you consider this data!  However, the mode makes perfect sense and is very easy to determine.

Range

While we're considering these methods of measuring central tendency, it would also be useful to mention range.  Technically, range doesn't provide any sense of measure of center.  However, it is very useful in evaluating the spread of the data, or how close the values are to the distribution's center.  Range is another simple concept, but it may not be exactly what you would think it should be.  If you have a dataset, or a graph of a distribution, you would be incorrect to say that the range is the low value to the high value.  (This would be similar to the definition of range in graphing, where range is all the y-values on the curve.)  However, range is slightly different in statistics.  Range is the DIFFERENCE between the high and low values of your dataset.  So, for the dataset 5, 6, 7, 10, 13, the range is 13-5, which is 8 (not 5 to 13, as may be thinking).

So, that is mean, median, mode, and range.  These are some of the most basic and common statistical operations that you will encounter.  Quite likely, you have already used some of these before, and may not have realized that you were actually doing statistical analysis of a dataset.  They are all different, and so they provide different assessments of how your data behaves.  They are all useful in their own way, and each shows strength in analyzing different types of data.  Therefore, it is extremely important that you learn what each stat means, and how to evaluate them.

I hope that this post has been informative and helpful for you!  If it was, please don't forget to hit the +1 button below, or click here to share by tweeting about it!